'전체 글'에 해당되는 글 5건
- 2020.04.07 :: 퀵 정렬(Quick sort) 1
- 2020.04.06 :: 버블 정렬(Bubble Sort)
- 2020.04.02 :: 삽입 정렬(Insertion Sort)
퀵 정렬은 기준값을 정해 그 값으로부터 작은 값은 왼쪽, 큰 값은 오른쪽으로 정렬한 뒤 분할을 반복하는 방식으로 순서는 아래와 같다.
1. 기준점을 하나 잡는다.
ㄴ이때 기준점은 어떤 값이든 상관 없다.
2. 오른쪽 먼저 오른쪽이 왼쪽보다 클 경우에만 반복하며, 해당 배열값이 기준점보다 크면 그 앞에 인덱스값을 비교한다.
3. 기준점보다 작은 값을 찾았을 경우 중지한다.
4. 이번에는 왼쪽을 시작하는데 오른쪽이 왼쪽보다 클 경우에만 반복하며, 기준점보다 작으면 그 뒤에 인덱스값을 비교한다.
5. 기준점보다 큰 값을 찾았을 경우 중지한다.
6. 오른쪽과 왼쪽의 인덱스값을 서로 바꾼다.
7. 이후 왼쪽의 값과 기준점을 바꾼다.
8. 배열의 시작부터 왼쪽 - 1 인덱스까지, 왼쪽 + 1인덱스부터 배열의 끝까지로 나눠 다시 정렬을 반복한다.
9. 최종적으로 배열의 크기가 1일때 정렬이 완료된다.
시간복잡도는 (배열의 크기)log(배열의 크기) 이다.

1행 - 기준값을 담을 변수
2, 3행 - 각각 왼쪽, 오른쪽 인덱스값을 담을 변수
14행 - 퀵정렬이 이루어지는 부분
17행 - 2~3번 과정
25행 - 4~5번 과정
33행 - 6번 과정
38행 - 7번 과정
42행 - 8번 과정
ㄴ각각 둘로 쪼개서 다시 퀵정렬을 돌리기 때문에 재귀함수로 호출한다.
'알고리즘 > 정렬' 카테고리의 다른 글
| 버블 정렬(Bubble Sort) (0) | 2020.04.06 |
|---|---|
| 삽입 정렬(Insertion Sort) (0) | 2020.04.02 |
| 선택 정렬(Selection Sort) (0) | 2020.04.01 |
버블 정렬은 연속된 두 개의 값을 비교해 기준에 해당하는 값을 뒤로 넘겨 정렬하는 방식이다.
그렇기에 맨 뒤에서부터 값이 완성되어 나가며 순서는 아래와 같다.
-오름차순 기준
1. 1번 인덱스와 2번 인덱스를 비교한다.
2. 1번 인덱스가 더 클 경우 서로 위치를 바꾼다.
3. 2번 인덱스와 3번인덱스를 비교한다.
4. 2,3 과정을 마지막 인덱스까지 반복한다.
5. 다시 1번부터 4번을 반복하되 마지막 인덱스 - 정렬 완료된 수만큼까지만 한다.
ㄴex) 2번째 사이클인 경우 첫번째 싸이클로 마지막값이 정렬 되 있으므로 그 앞에까지만 돌린다.
시간복잡도는 (배열의 크기) * (n^2)이다.

코드로 구현 시 이렇게 되며, 여기에
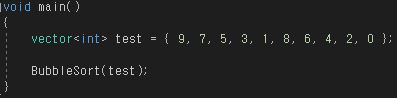
다음과 같은 배열을 입력 시

다음과 같은 결과가 나온다.
간단하게 두 번째 사이클 첫번째 과정까지만 진행 순서를 보자.
1. 0번 인덱스(9)와 1번 인덱스(7)를 비교한다.
2. 0번 인덱스(9)가 더 크므로 두 인덱스간 값을 바꾼다.
ㄴ이 과정으로 0번인덱스는 7, 1번 인덱스는 9가 된다.
3. 1번 인덱스(9)와 2번 인덱스(5)를 비교한다.
4. 1번 인덱스(9)가 더 크므로 두 인덱스간 값을 바꾼다.
5. 이 과정을 마지막 인덱스까지 반복해 9번 인덱스의 값이 9가 되었다.
ㄴ여기서 한 싸이클이 끝난다.
6. 0번 인덱스(7)와 1번 인덱스(5)를 비교한다.
7. 0번 인덱스가 값이 더 크므로 두 인덱스간 값을 바꾼다.
8. 이 과정을 반복하되, 이미 값 하나가(1~5과정) 맨 끝에서 정렬이 되어 있으므로 그 앞에까지만 진행한다.
ㄴ즉, 현재 싸이클 - 1만큼 진행한다 생각하면 된다.
'알고리즘 > 정렬' 카테고리의 다른 글
| 퀵 정렬(Quick sort) (1) | 2020.04.07 |
|---|---|
| 삽입 정렬(Insertion Sort) (0) | 2020.04.02 |
| 선택 정렬(Selection Sort) (0) | 2020.04.01 |
삽입 정렬은 현재 위치에서 자신 앞에 있는 배열들과 값을 비교 해 들어갈 위치를 찾는 방식으로 순서는 아래와 같다.
1. 배열의 두 번째 값을 선택한다.
2. 선택 된 값과 자신 앞의 값을 비교한다.
3. 앞의 값이 자신보다 작으면 그 자리에 멈추고, 클 경우 그 앞의 값을 비교한다.
4. 앞의 값이 자신보다 작거나 배열 첫 번째 값까지 2, 3번 과정을 반복한다.
최악의 경우는 선택 정렬과 마찬가지로 배열의 크기 * (n^2)의 시간복잡도 이지만, 이미 정렬이 되어 있는 경우에는 배열의 크기만큼의 시간 복잡도를 가진다.
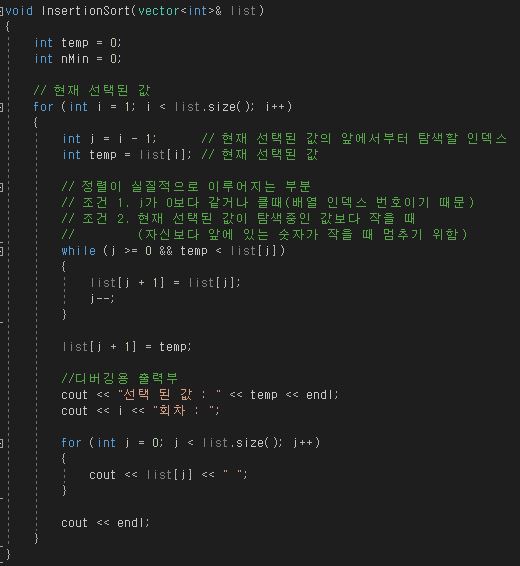
코드로 구현 시 이렇게 되며, 여기에
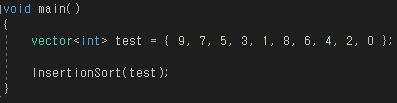
다음과 같은 배열을 넣을 시

다음과 같은 결과값이 나온다.
간단하면서 과정을 보기 위해 3번 인덱스만 진행 순서를 보자.
0. 2번 인덱스까지의 작업으로 배열은 5, 7, 9, 3, 1, 8, 6, 4, 2, 0으로 되어 있다.
1. 3번 인덱스(3)의 값이 선택된다.
2. 2번 인덱스(9)과 비교해 값이 더 작으므로 1번 인덱스(7)와 비교한다.
3. 1번 인덱스(7)보다도 더 작으므로 0번 인덱스(5)와 비교한다.
4. 0번 인덱스(5)보다 더 작으므로 3번 인덱스를 0번 인덱스로 이동한다.
5. 그러므로 배열은 3, 5, 7, 9, 1, 8, 6, 4, 2, 0이 된다.
코드상으로는 따로 값을 담아주지만, 간단하게 생각하면 들어갈 위치에 넣고 뒤에를 다 원래 자신이 있던 위치까지 밀어준다고 생각하면 된다.
'알고리즘 > 정렬' 카테고리의 다른 글
| 퀵 정렬(Quick sort) (1) | 2020.04.07 |
|---|---|
| 버블 정렬(Bubble Sort) (0) | 2020.04.06 |
| 선택 정렬(Selection Sort) (0) | 2020.04.01 |
